PUZZLES

TANGRAM

The ancient Chinese story of the tangram is that a sage, a wise old man was to take a precious sheet of glass to the king who needed a window in his palace. The square piece of glass was wrapped in silk and canvas and carried in the sage’s backpack. The journey was long, the sage crossed a desert and rivers, and he travelled through forests and fields. He arrived at a rugged mountain range and climbed to the summit of a high, rocky peak. At the top of the mountain he looked into the distance and glimpsed the palace.

Pleased that he had almost arrived, he stumbled and tumbled down the side of the mountain. The glass was broken.  When he met the king he told of his journey and admitted that the glass was broken. The square glass was unwrapped from its silk and canvas case and the sage was surprised to see that glass was not shattered but divided into seven geometric shapes.

The sage moved the shapes around and made images to describe his journey.

He showed the king his home, a camel he had seen in the desert, monks he met on his way, a boat on the river he crossed and the mountain range where he fell.

8 QUEEN PUZZLE

 This puzzle played on a chess board (8 x 8 grid) requires 8 queens any pieces can be used to represent the queen and the problem is to place all of the queens on the board without a connecting horizontal vertical or diagonal line there are 92 distinct solution to this problem one is shown here.This problem can also be tried on different size grids, and the connection between grid size and number of solutions looked into.

SOLUTION 8 QUEEN PROBLEM          MAGIC SQUARE ORDER 3(15)       ANCIENT MAGIC SQUARE KNOTS FOR NUMBERS      MAGIC SQUARE ORDER 5 (65)

MAGIC SQUARE

Magic Squares are square grids with a special arrangement of numbers in them. These numbers are special because every row, column and diagonal adds up to the same number. So for the  3 x 3 grid , 15 is the magic number. Could you work this out just from knowing that the square uses the numbers from 1 to 9? If numbers 1 to 9 are cut out of cardboard and placed in the spaces various activities are possible. Also with the addition of mathematical symbols or letters or  mathematical symbols  the squares can be used to form other math and letter games..

The two numbers that are opposite each other across the centre number will add up to the same number. This is only true in the  3 X 3 square  e.g.  8 + 2 = 10, 6 + 4 = 10  etc.

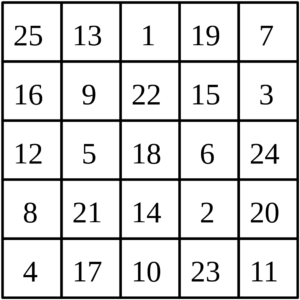
The order of the magic square is the number of rows and colums it has so an example of a solution for an order 5 magic square number 1 to 25 are used and the magic number is 65

From ancient times  magic square were connected with the supernatural . The earliest record of magic squares is from China in about 2200 BC. and is called “Lo-Shu”. There’s a legend that says that the Emperor Yu saw this magic square on the back of a divine tortoise in the Yellow River. The black knots show even numbers and the white knots show odd numbers. Look closely and you’ll see that this ancient magic square is the same as our example above. Magic squares were first mentioned in the Western world in the work of Theon of Smyrna. They were also used by Arab astrologers in the 9th century to help work out horoscopes. The work of the Greek mathematician Moschopoulos in 1300 A.D. help to spread knowledge about magic squares.

Students can practice making their own magic squares and looking for patterns.